5 Major Sorting Algorithms

Sorting is a common task that you come across while programming a variety of applications. For instance, sort a list of products in ascending order of price, sort a result in descending order based on relevance value, and so on.

While in school, I had learnt a few simple ways to sort an array. If I am remembering correctly, it was the 'Bubble Sort' or something like that. Recently, I decided to take another look at it. And it was a refreshing experience. In this blog, I am sharing a few things I've learnt about it.

Most programming languages come with sorting functions out of the box. For instance, in JavaScript, you can use the Array.prototype.sort() method to sort an array in ascending order.

So, why would you even want to learn sorting algorithms? That's the question.

Why learn sorting algorithms

Even if programming languages offer built-in functions for sorting, learning how to do it from scratch has many advantages. Here are some I can think of:

• Deepens your knowledge in concepts like recursion, performance optimisation, etc.
• If a need comes where you can't use a built-in function, you will be able to do it yourself.
• Inspires you to think about the performance difference between various algorithms, which can help optimise your programs better.
• After all, it is fun - you can try them out on piece of paper. No need to code everything out. Write down some random numbers (that's an array), these try sorting them manually using these techniques. Then figure out which one feels faster for you. It'll be a fun game for kids also.

Major sorting algorithms

1. Selection Sort

Selection sort algorithm works by finding the next lowest item in the array and moving it to the front. So after the first iteration, you'll have the lowest item at the zeroth index, after the second iteration, the second lowest item will be at index 1, and so on until it finishes.

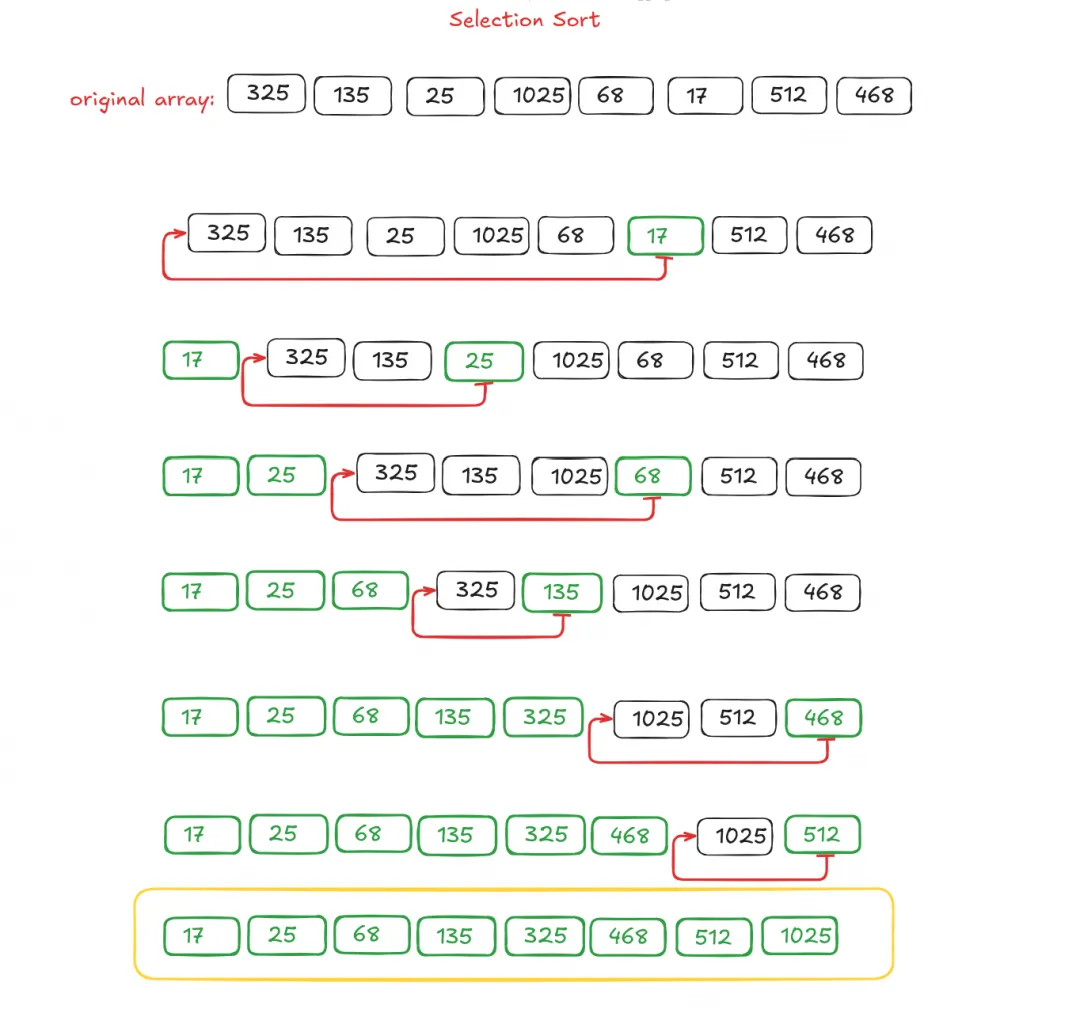
Since it involves two levels of iteration, the execution time is proportional to the square of the number of items, just like Bubble sort. So it is definitely not the fastest sorting algorithm.

• Time complexity (best): O(n^2)
• Time complexity (average): O(n^2)
• Time complexity (worst): O(n^2)
• Space complexity: O(1)
• Stable: No

2. Bubble Sort

Bubble sorting works by comparing adjacent elements from left to right and swapping them if required. By the end of the first iteration, the largest element will be at the end of the array. It feels like "bubbling" the largest element towards the right in each step, hence the name.

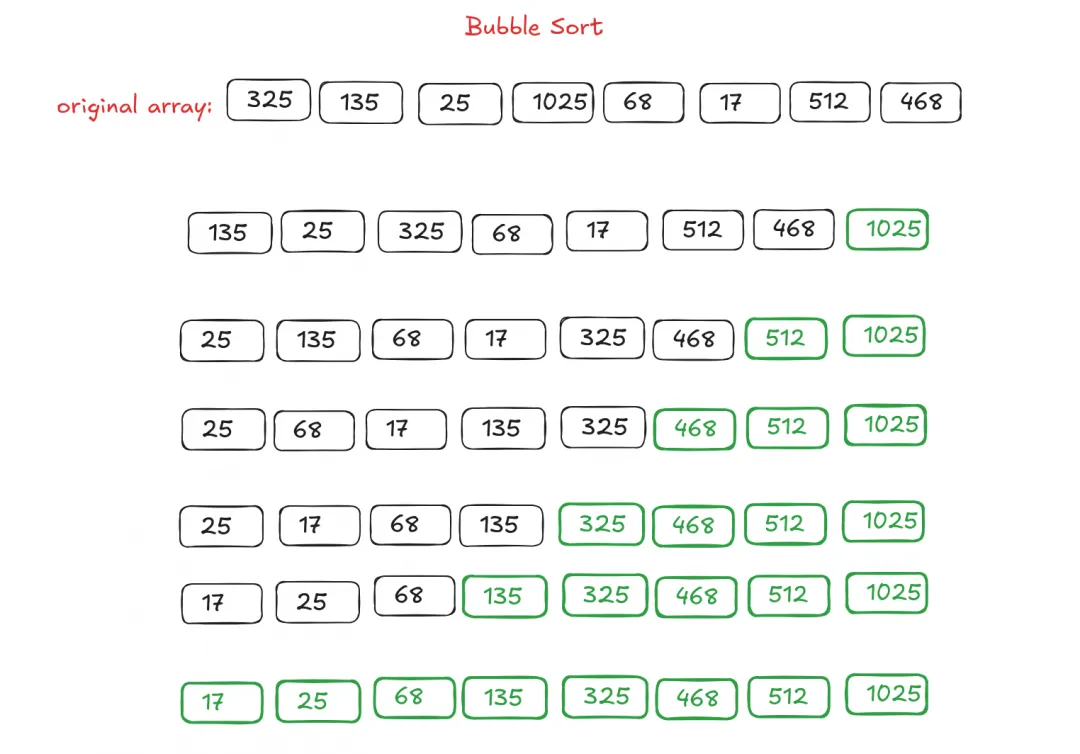
As far as I've learnt, bubble sort is probably the slowest. But in the best case, where the array is sorted early, it can be faster by skipping the remaining comparisons. You can add flag to to check this condition, where an iteration gets finished without any swapping.

• Time complexity (best): O(n)
• Time complexity (average): O(n^2)
• Time complexity (worst): O(n^2)
• Space complexity: O(1)
• Stable: Yes

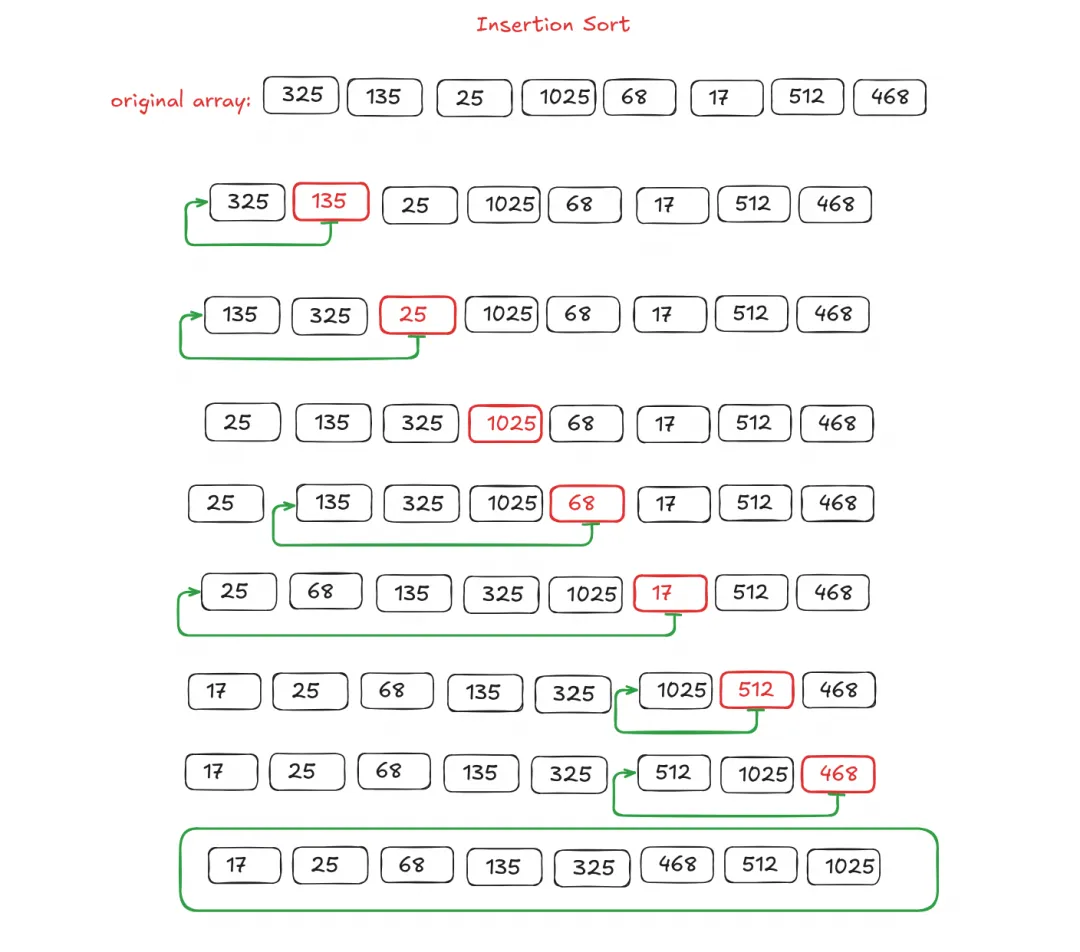
3. Insertion Sort

Insertion sort works by inserting each element into the correct position among the sorted previous elements. It starts by comparing the second element with the first element, and moving it forward to give place at zeroth index, if second element is smaller than the first element. So after the first step, the first and second elements will be sorted.

In the next step, the next item - that is the third element - will be compared with the sorted first and second elements to find its correct position. After that step, the first three elements will be sorted. Like that it goes until all the elements are sorted.

• Time complexity (best): O(n)
• Time complexity (average): O(n^2)
• Time complexity (worst): O(n^2)
• Space complexity: O(1)
• Stability: Yes

4. Merge Sort

Merge sort is an algorithm that implements the divide-and-conquer technique. It divides an array until it cannot be divided further (that is, only one element), then merges them together while sorting the elements to correct positions. This is done recursively, which is the magic.

An array with one element is already sorted. Hence it is easy to form a sorted 2-element array by sorting two such 1-element arrays - just one swap. Now, it is easy to merge two such sorted 2-element arrays to form a sorted 4-element array. Just keep comparing the left-most elements, the lowest is moved to the result array, and the index pointer is incremented for the array from which the lowest element is taken. And it goes like that until the whole array is fully merged back.

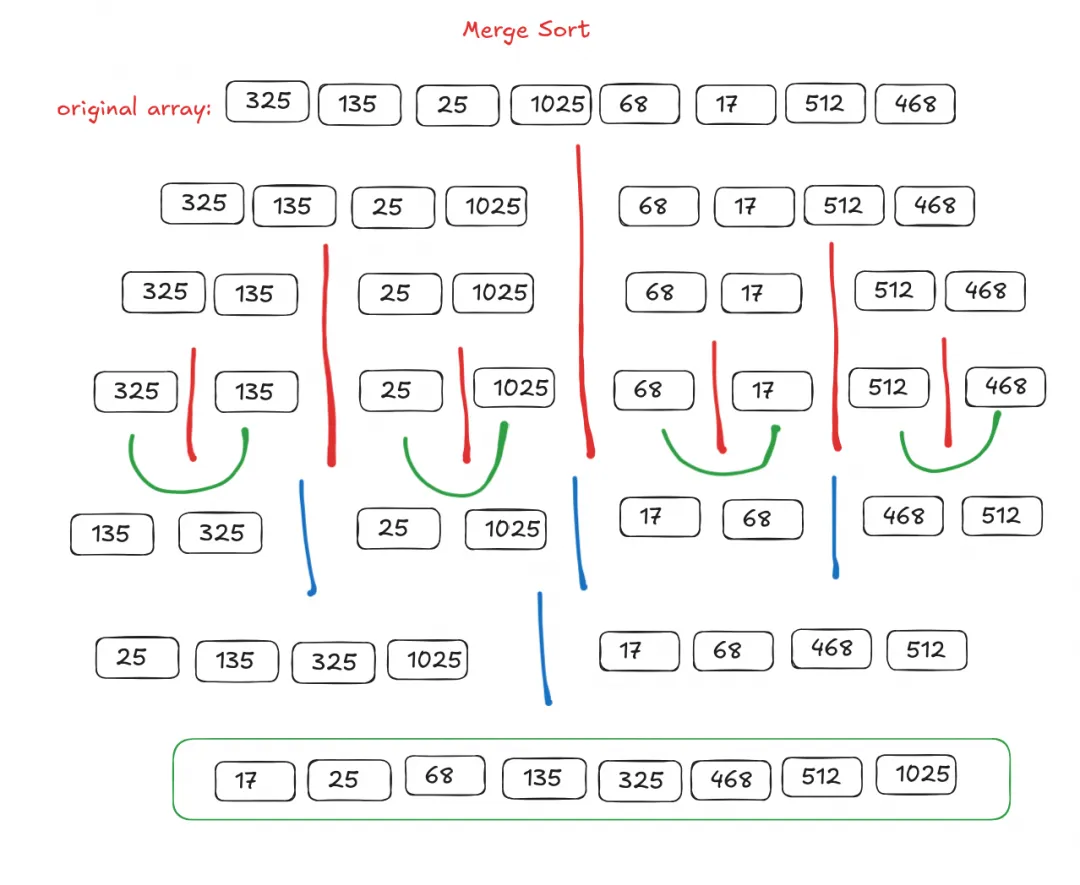
Merge sort is a fast and stable algorithm. So it is a good choice for most purposes.

• Time complexity (best): O(n log n)
• Time complexity (average): O(n log n)
• Time complexity (worst): O(n log n)
• Space complexity: O(n)
• Stability: Yes

5. Quick Sort

Quick sort is another algorithm that uses the divide-and-conquer technique. It starts by picking a pivot element, then moves each of the other element to the left or right of it, based on whether it is smaller or larger respectively. The pivot can be any element chosen randomly. Another common way is to choose the first or last element as the pivot.

Then the process is repeated for the left part and right part, recursively, until there is only one element in the array. By then the array will be sorted.

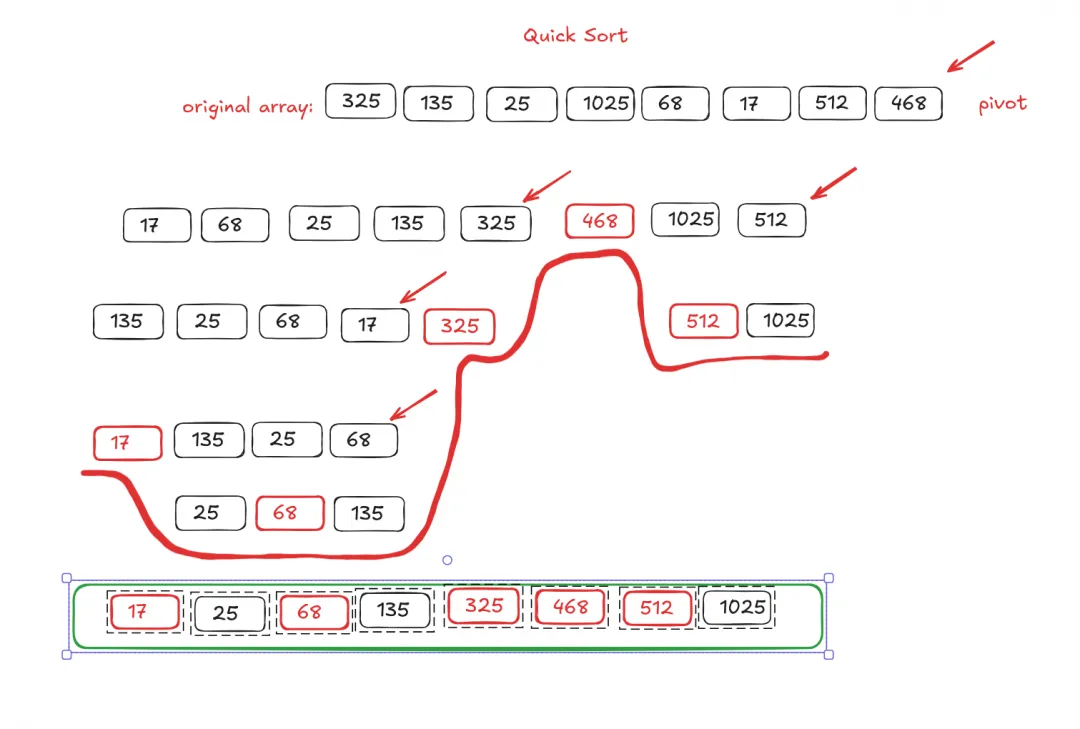
Quick sort is also quite fast like merge sort. When I tested it on a randomly generated array with one million elements, quick sort consistently performed faster than merge sort.

However, the downside is that it is not stable. When the elements are moved left or right to the pivot, the relative order gets disrupted. So it may not be good for multi-level sorts - for e.g., sort alphabetically and numerically.

Also, if the pivot choice is poor, the performance can degrade. In the worst case, it can be as slow as selection, bubble, and insertion sorts.

• Time complexity (best): O(n log n)
• Time complexity (average): O(n log n)
• Time complexity (worst): O(n^2)
• Space Complexity: O (n log n)
• Stability: No

Time and Space Complexities, Stability

+-----------+------------+--------+----------+-----------+------------+
| Algorithm | Best     | Avg.     | Worst    | space     | Stability  |
|           |          |          |          | complexity|            |
+-----------+------------+--------+----------+-----------+------------+
| Selection | O(n^2)   | O(n^2)   | O(n^2)   | O(1)      | unstable   |
| Bubble    | O(n)     | O(n^2)   | O(n^2)   | O(1)      | stable     |
| Insertion | O(n)     | O(n^2)   | O(n^2)   | O(1)      | stable     |
| Merge     | O(nlogn) | O(nlogn) | O(nlogn) | O(n)      | stable     |
| Quick     | O(nlogn) | O(nlogn) | O(n^2)   | O(logn)   | unstable   |
+-----------+------------+--------+----------+-----------+------------+

Time and Space Complexities

The above values that look like O(n^2), O(n log n), etc are called 'Big O' notation. The Best, Avg, and Worst values represents the 'Time complexity' - that is the relative time required to run the sorting program for an array with n number of elements.

So, O(n^2) means the time is proportional to the square of the number of elements. Whereas O(n log n) is smaller (faster), or has less complexity, because n is being multiplied with log n, which will be always smaller than n.

Similarly, 'Space Complexity' simply refers to the amount of memory required to run the sorting program.

Why Stability Matters

Then comes the 'Stability'. A sorting algorithm is said to be stable, if if preserves the relative order of identical values in the sorted result.

For instance, sometimes an array contains both string and number values. And we need to sort both alphabetically and numerically, with preference for the latter. Let's take an example array:

{apples: 25, mangoes: 25, oranges: 7, strawberries: 40}

The array is currently sorted alphabetically - a < m < o < s;

Now if it is sorted numerically in ascending order, the result should be:

{oranges: 7, apples: 25, mangoes: 25, strawberries: 40}

oranges is moved to the zeroth index because it has the lowest count. At the same time the relative order of apples and mangoes are preserved, both of which have the same count. So they are still alphabetically sorted.

But if you use an unstable algorithm like Selection Sort, that won't be the result. Instead you'll get:

{oranges: 7, mangoes: 25, apples: 25, strawberries: 40}

If you're not sure, try programming it.

Here, the relative order of mangoes and apples are changed, which messes up the initial alphabetical sort.

This won't happen with stable algorithms that swaps only adjacent elements. Because it won't cross position with a distant element with identical numerical value.

Conclusion

We discussed the five major sorting algorithms. But I know that there are others too, like Radix sort, Tim Sort, Heap Sort, etc. Maybe I can add them also at a later time.